Abstract
Real-world robotic agents must act under partial observability and long horizons, where key cues may appear long before they affect decision making. However, most modern approaches rely solely on instantaneous information, without incorporating insights from the past. Standard recurrent or transformer models struggle with retaining and leveraging long-term dependencies: context windows truncate history, while naive memory extensions fail under scale and sparsity.
We propose ELMUR (External Layer Memory with Update/Rewrite), a transformer architecture with structured external memory. Each layer maintains memory embeddings, interacts with them via bidirectional cross-attention, and updates them through an Least Recently Used (LRU) memory module using replacement or convex blending.
ELMUR extends effective horizons up to 100,000 times beyond the attention window and achieves a 100% success rate on a synthetic T-Maze task with corridors up to one million steps. In POPGym, it outperforms baselines on more than half of the tasks. On MIKASA-Robo sparse-reward manipulation tasks with visual observations, it nearly doubles the performance of strong baselines. These results demonstrate that structured, layer-local external memory offers a simple and scalable approach to decision making under partial observability.
Method
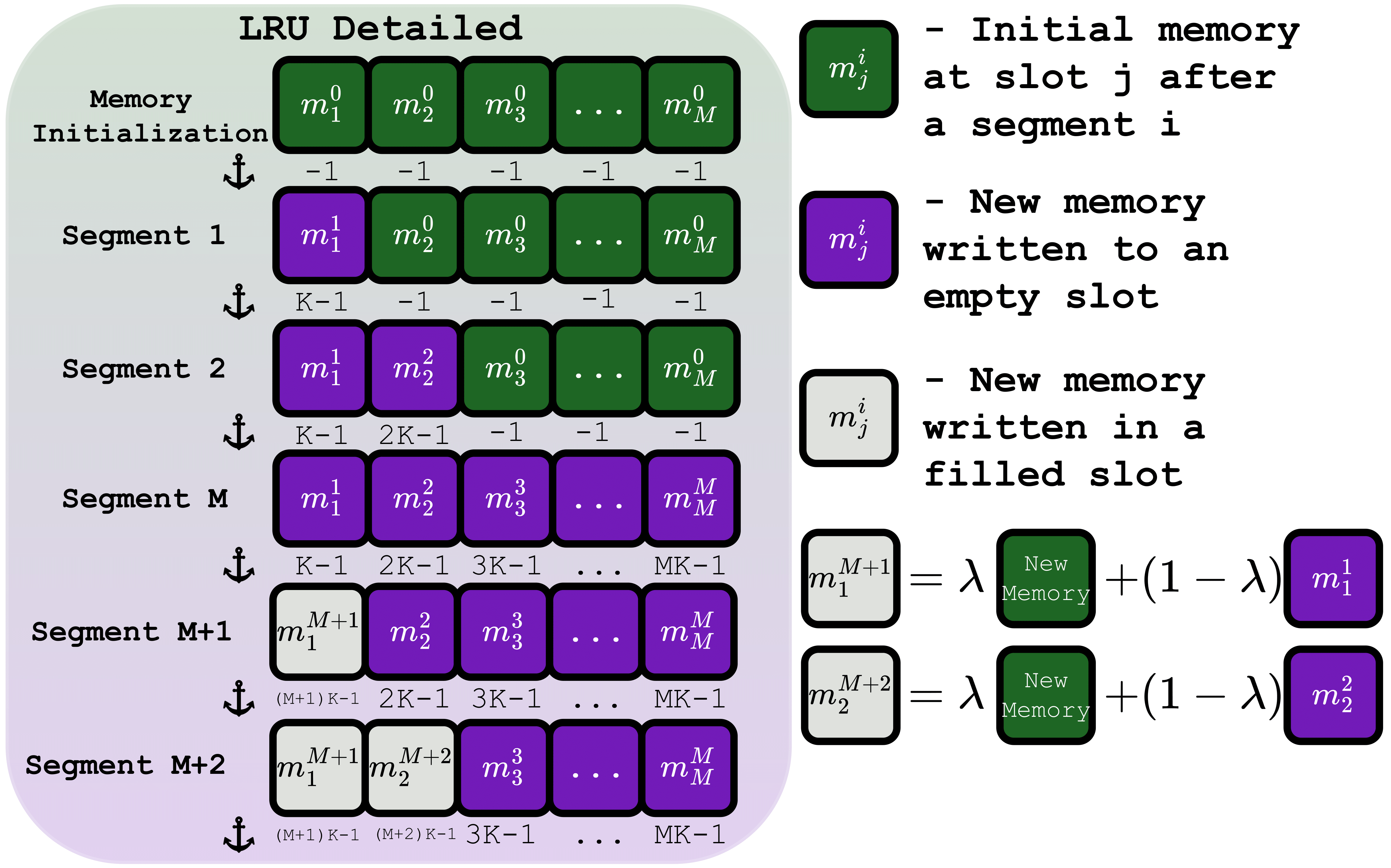
LRU: fill empty slots, then blend updates into the least-recently-used slot.
Long-horizon, partially observed tasks need persistent memory beyond a fixed attention window. ELMUR augments each Transformer layer with layer-local external memory with cross-attention-based read–write operations managed by an Least Recently Used (LRU) policy which selectively updates memory via replacement or convex blending.
Segment-Level Recurrence
A trajectory of length \(T\) is split into \(S=\lceil T/L\rceil\) segments \(\mathcal{S}_i\) (context \(L\)). Each segment reads the previous memory (detached) and updates it, where \(\mathbf{h}^{(i)}\) represents the token embeddings at segment \(i\) and \(\mathbf{m}^{i-1}\) represents the memory embeddings from the previous segment:
\[ \mathbf{h}^{(i)}=\mathrm{TokenTrack}\!\big(\mathcal{S}_i,\operatorname{sg}(\mathbf{m}^{\,i-1})\big). \]
Token Track (Read)
Tokens model local structure with self-attention and read from memory via cross-attention:
\[ \mathbf{h}_{\text{sa}}=\mathrm{AddNorm}\!\big(\mathbf{x}+\mathrm{SelfAttention}(\mathbf{x})\big), \] \[ \mathbf{h}_{\text{mem2tok}}=\mathrm{AddNorm}\!\big(\mathbf{h}_{\text{sa}}+\mathrm{CrossAttention}(Q{=}\mathbf{h}_{\text{sa}},K,V{=}\mathbf{m})\big), \] \[ \mathbf{h}=\mathrm{AddNorm}\!\big(\mathbf{h}_{\text{mem2tok}}+\mathrm{FFN}(\mathbf{h}_{\text{mem2tok}})\big). \]
Memory Track (Write)
Memory is updated from tokens via cross-attention and FFN:
\[ \mathbf{m}_{\text{tok2mem}}=\mathrm{AddNorm}\!\big(\mathbf{m}+\mathrm{CrossAttention}(Q{=}\mathbf{m},K,V{=}\mathbf{h})\big), \] \[ \mathbf{m}_{\text{new}}=\mathrm{AddNorm}\!\big(\mathbf{m}_{\text{tok2mem}}+\mathrm{FFN}(\mathbf{m}_{\text{tok2mem}})\big). \]
Relative Bias (Read/Write)
Cross-attention uses a learned relative bias to encode token–memory offsets:
\[ \mathrm{Attn}(\mathbf{Q},\mathbf{K})=\frac{\mathbf{Q}\mathbf{K}^\top}{\sqrt{d_h}}+\mathbf{B}_{\text{rel}}, \qquad \mathbf{B}_{\text{rel}}= \begin{cases} \mathbf{E}[t{-}p]\in\mathbb{R}^{B\times H\times L\times M} & \text{read (mem2tok)}\\[4pt] \mathbf{E}[p{-}t]\in\mathbb{R}^{B\times H\times M\times L} & \text{write (tok2mem)} \end{cases} \]
LRU Memory Update (Bounded & Persistent)
Empty slots are filled; otherwise the least-recently-used slot is refreshed by convex blending:
\[ \mathbf{m}^{\,i+1}_j=\lambda\,\mathbf{m}^{\,i+1}_{\text{new}}+(1-\lambda)\,\mathbf{m}^{\,i}_j,\quad \lambda\in[0,1]. \]
This yields scalable, temporally grounded memory with constant compute per segment.
Experimental Results
We evaluate ELMUR on three memory-intensive benchmarks with partial observability: T-Maze (synthetic long-horizon recall), POPGym-48 (33 memory puzzles + 15 reactive control tasks), and MIKASA-Robo (sparse-reward robotic manipulation with RGB observations). Unless noted, results aggregate 3 runs (4 for T-Maze), 100 eval seeds per run, reported as mean ± SEM.
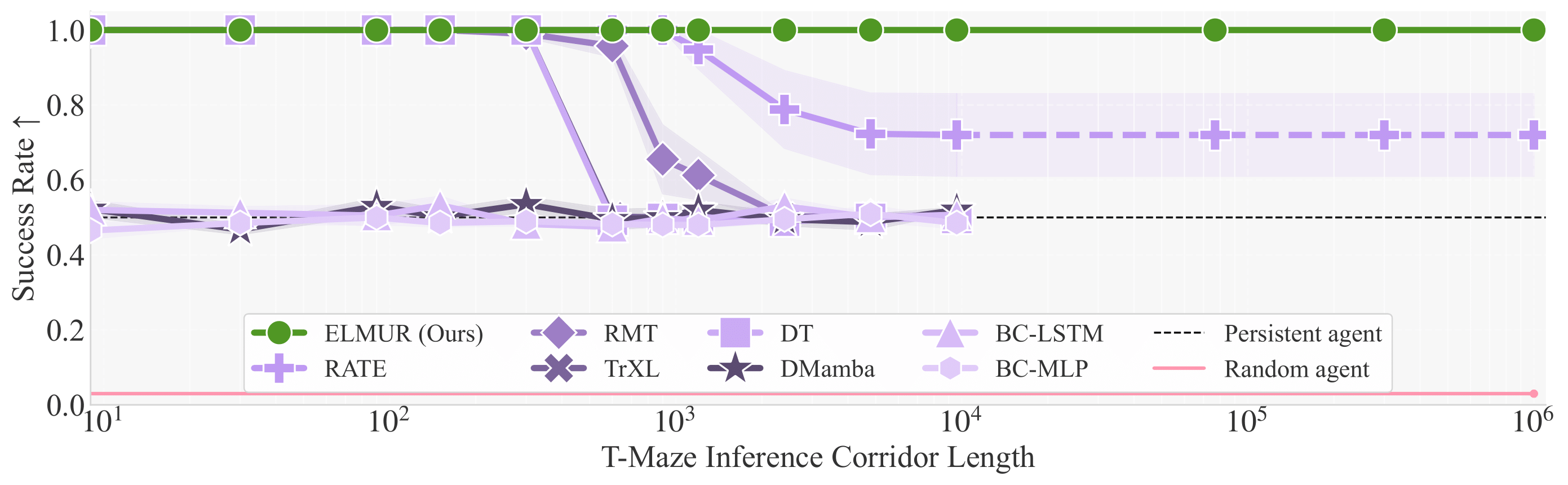
T-Maze: Long-Horizon Retention
Success rate on the T-Maze task as a function of inference corridor length. ELMUR achieves a 100% success rate up to corridor lengths of one million steps. In this figure, the context length is L=10 with S=3 segments; thus ELMUR carries information across horizons 100,000 times longer than its context window.
Despite being trained with a short attention window (L=10), ELMUR maintains perfect success as the corridor length increases from \(10^2\) to \(10^6\) steps, while standard sequence models rapidly degrade once the horizon exceeds their window. This shows that the external layer memory, not the attention cache, carries the cue over extreme delays.
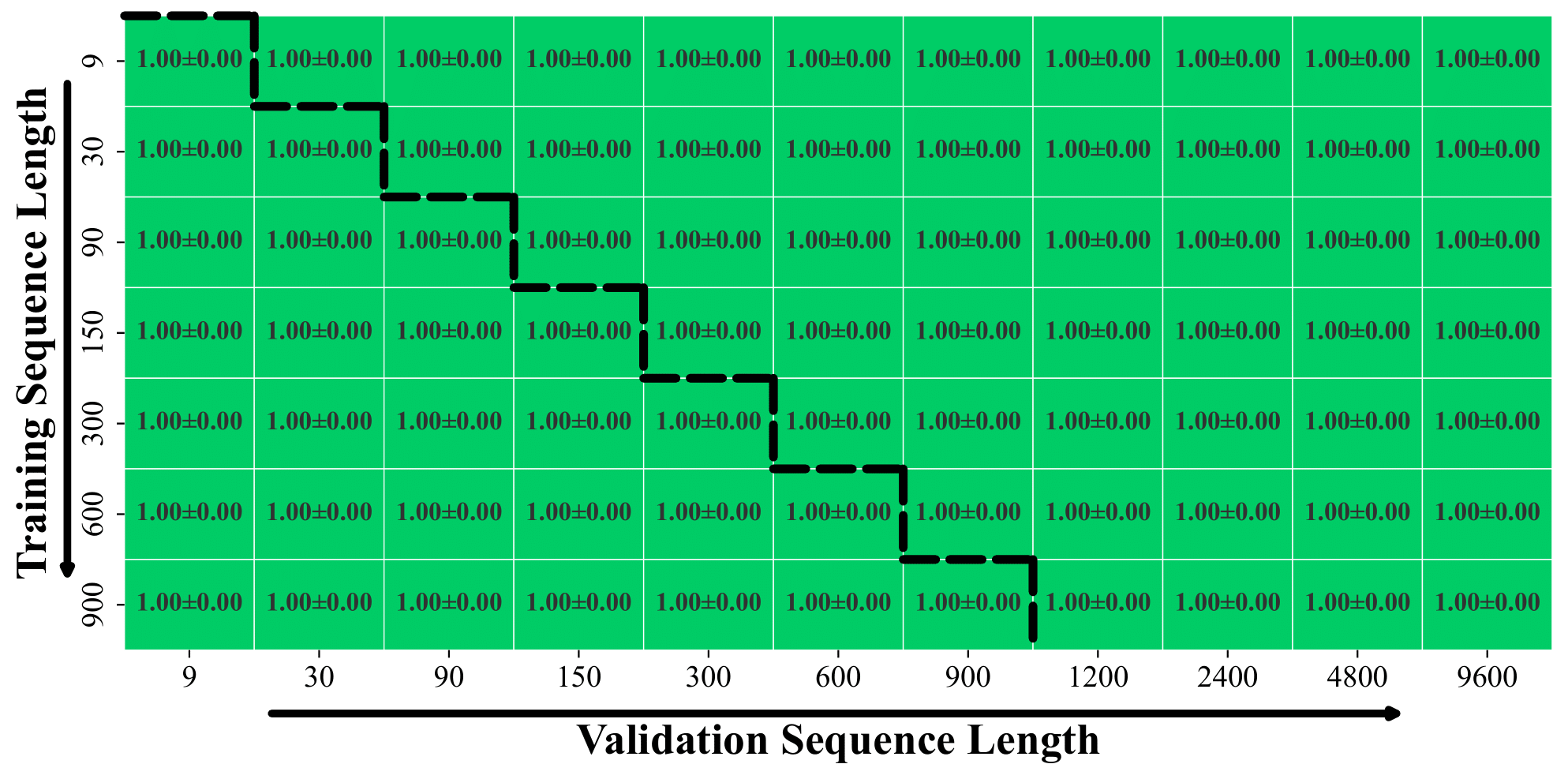
Generalization of ELMUR across T-Maze lengths. Each cell shows success rate (mean ± standard error) for training vs. validation lengths. ELMUR transfers perfectly: models trained on shorter sequences retain 100% success up to 9600 steps. Training lengths were split into three equal segments.
Models trained on short sequences (9–900 steps) extrapolate to much longer ones (up to 9600) without loss, and also interpolate to shorter lengths. This indicates that the learned read–write policy and relative bias remain stable across scales.
POPGym-48: Broad Generalization
Aggregated returns over all 48 POPGym tasks. ELMUR ranks first on 24/48 tasks, with the largest gains on memory puzzles.
ELMUR achieves the best overall score on POPGym (10.4), driven by clear gains on the puzzle subset, while remaining competitive on reactive control. The improvements concentrate on tasks requiring long-term recall, validating the role of layer-local memory.
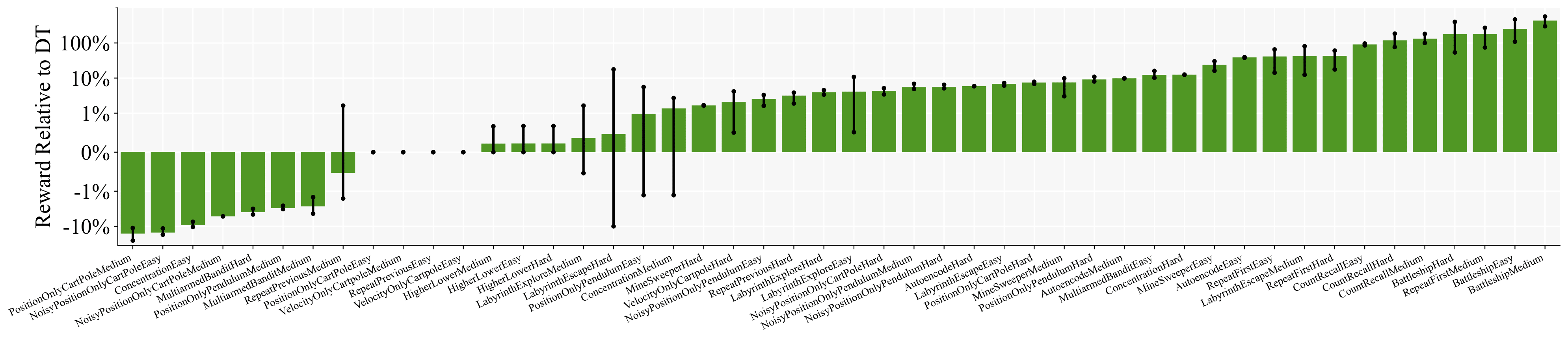
ELMUR compared to DT on all 48 POPGym tasks. Each model was trained with three independent runs, validated over 100 episodes each. Bars show the mean performance with 95% confidence intervals computed over these three means. ELMUR achieves consistent improvements over DT, with the largest gains on memory-intensive puzzles.
MIKASA-Robo: Visual Manipulation
Success rates on MIKASA-Robo tasks. ELMUR nearly doubles the performance of strong baselines.
On sparse-reward manipulation, ELMUR attains
RememberColor3/5/9-v0 = 0.89 ± 0.07, 0.19 ± 0.03, 0.23 ± 0.02, and
TakeItBack-v0 = 0.78 ± 0.03, substantially above the best baselines (e.g., RATE 0.42 ± 0.24 on TakeItBack).
The gains persist as distractors increase, suggesting that persistent per-layer memory resists visual interference better than windowed attention.
Takeaways.
1. ELMUR preserves task-relevant information across horizons far beyond the attention window;
2. ELMUR generalizes seamlessly to unseen sequence lengths;
3. ELMUR improves robotic manipulation with pixel observations;
4. ELMUR scales to diverse POPGym tasks without trading off reactive control.
Poster
BibTeX
@misc{cherepanov2025elmurexternallayermemory,
title={ELMUR: External Layer Memory with Update/Rewrite for Long-Horizon RL},
author={Egor Cherepanov and Alexey K. Kovalev and Aleksandr I. Panov},
year={2025},
eprint={2510.07151},
archivePrefix={arXiv},
primaryClass={cs.LG},
url={https://arxiv.org/abs/2510.07151},
}